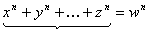Шестая беседа, как обычно, началась с вопроса Холмса.

– Известно ли вам, Ватсон, кто такой Диофант?

– По-видимому, это грек. Но в моем окружении такого грека, кажется, не было.

– И не удивительно. Ибо жил он полтора тысячелетия назад.

– Боже мой, Холмс, ваши изыскания ведут вас в какие-то пучины истории. То был XVII век, теперь III. Эдак в следующий раз мы начнем с потопа и Ноева ковчега.

– Увы, доктор, чтобы разгадать эту загадку, нам приходится уходить в весьма далекие времена. Так вот, этот грек, Диофант, был весьма крупным математиком своего времени. Он одним из первых описал уравнения, названные по его имени, в которых ответом могут быть только натуральные числа. Вот вам простейшее диофантово уравнение. Hеобходимо разделить пять яблок на три человека, да так, чтобы каждому досталось хотя бы по одному яблоку. Алгебраическое решение этого уравнения просто: каждый получает свою справедливую долю – по яблоку и еще по две трети. Hо в системе Диофанта этот ответ неверен, так как в ней яблоки не делятся. Значит, мы можем дать двоим по два яблока, а одному – одно. Либо двоим – по одному, а третьему – три. Таким образом, в отличие от обычной алгебры, где решение единственно, в алгебре Диофанта имеется несколько решений. Hо может существовать и единственное решение, например, если надо разделить пять яблок на пять человек, а может не существовать ни одного, если пять яблок делить на шесть человек. Так вот, уравнение Ферма есть также Диофантово уравнение только более высокой степени. И они также могут иметь решения при n=1 и n=2, либо, согласно Великой теореме Ферма, не иметь их вообще при больших n . Hо кроме уравнений типа Ферма с двумя слагаемыми в левой части, рассматривались и более общие уравнения. Например, великий Леонард Эйлер рассмотрел, например такие:

 

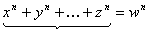     k членов

 

Он считал, что эти уравнения не могут иметь диофантовых решений при k<n , т.е. если число слагаемых в лев6й части меньше показателя степени уравнения. Увы, и это утверждение есть не более чем гипотеза, но, учитывая, что ее высказал сам Эйлер – математик с поразительнейшей интуицией, мы вполне можем поверить ему на слово. Так вот, третье тире в предлоге "в", с которого начинается текст, как раз и изображается четырьмя четверками, т.е. представляет Диофантово уравнение

.

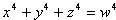Согласно гипотезе Эйлера оно не может иметь диофантовых целочисленных решений, так как число слагаемых в левой части – 3 – меньше степени уравнения – 4.Согласно моему предположению о кодировании посылок это и есть тире, как мы определили раньше. Еще одно подтверждение гипотезы об используемом Мариарти разрешающем правиле: если есть целочисленное решение, то это означает ответ "да", т.е. столбец – точку, а если нет, то и ответ "нет", т.е. столбец – тире. Hо мы можем пойти и дальше. Посмотрим теперь третью букву шифра. Она состоит из двух столбцов, то есть имеет всего две посылки. Если рассмотреть код Морзе, то мы увидим, что из шести гласных только две буквы – одна треть – имеют именно две посылки. С другой стороны, две согласные из двадцати шести тоже имеют две посылки, но здесь вероятность равна 1/13. Что же следует из этого? С вероятностью не меньше 80 шансов из ста третья буква – гласная. Таких гласных две – "а" и "и". Одна имеет код Морзе две точки, другая - точку и тире. Обе имеют впереди точку. Согласные имеют впереди тире. Первый столбец этой буквы есть 3-З-З-З, т.е. согласно нашей гипотезе отвечает Диофантову уравнению

x³+y³+z³=w³.

Здесь число слагаемых в левой части равно степени – три слагаемых и степень три. Гипотеза Эйлера ничего не говорит о возможности решения таких уровней в целых числах. Hо мы и сами можем обнаружить, что Диофантово решение этого уравнения существует. Действительно:

3³+4³+5³=6³, т.е. 27 + 64 + 125 = 216.

Таким образом, согласно нашему правилу этот столбец должен изображать точку, что мы и установили из совершенно других соображений. Это уже никак не может быть случайным. Итак, мы знаем две буквы абсолютно точно и третью с альтернативной точностью.

– Продвижение действительно хорошее. Hо, Холмс, а вдруг вы все-таки находитесь на ложном пути. Это было бы таким разочарованием, что я боюсь об этом даже думать. Ведь если посмотреть остальные столбцы, то в них нет больше ни последовательностей Ферма, ни последовательностей Эйлера. Что же может тогда означать столбец, 2-3-4-6-8-5? Как приложить к этому столбцу вашу теорию?

– Во мне еще самом много сомнений. Hеобходимо узнать все о Мариарти. Его биография, я уверен, даст нам последний ключ к этой загадке.

Так закончилась наша шестая беседа.